 | Feshbach, Daniel; Chen, Wei-Hsi; Xu, Ling; Schaumburg, Emil; Huang, Isabella; Sung, Cynthia Algorithmic Design of Kinematic Trees Based on CSC Dubins Planning for Link Shapes (Conference) Workshop on the Algorithmic Foundations of Robotics (WAFR), 2024. @conference{feshbach2024kinematicTrees,
title = {Algorithmic Design of Kinematic Trees Based on CSC Dubins Planning for Link Shapes},
author = {Daniel Feshbach and Wei-Hsi Chen and Ling Xu and Emil Schaumburg and Isabella Huang and Cynthia Sung},
url = {https://repository.upenn.edu/handle/20.500.14332/60660
https://www.algorithmic-robotics.org/papers/43_Algorithmic_Design_of_Kinem.pdf},
year = {2024},
date = {2024-10-08},
urldate = {2024-10-08},
booktitle = {Workshop on the Algorithmic Foundations of Robotics (WAFR)},
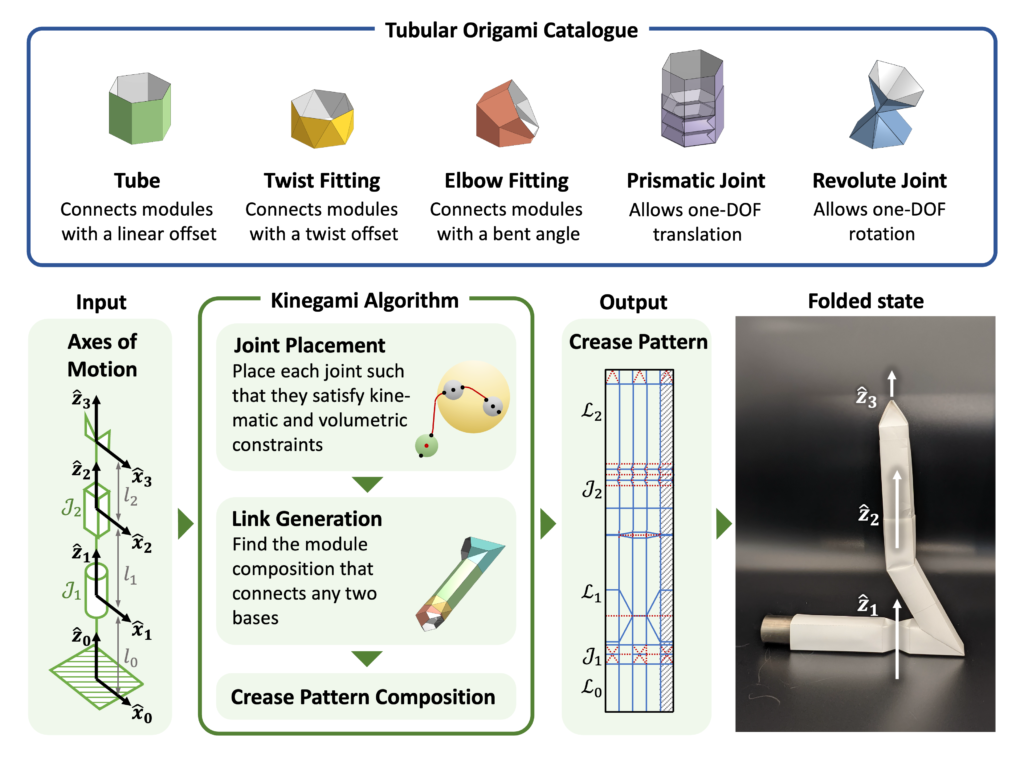
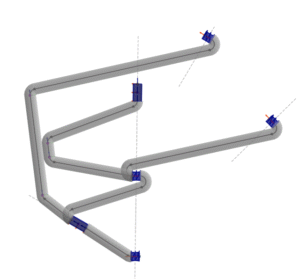
abstract = {Computational tools for robot design require algorithms moving between several layers of abstraction including task, morphology, kinematics, mechanism shapes, and actuation. In this paper we give a linear-time algorithm mapping from kinematics to mechanism shape for tree-structured linkages. Specifically, we take as input a tree whose nodes are axes of motion (lines which joints rotate about or translate along) along with types and sizes for joints on these axes, and a radius $r$ for a tubular bound on the link shapes. Our algorithm outputs the geometry for a kinematic tree instantiating these specifications such that the neutral configuration has no self-intersection. The algorithm approach is based on understanding the mechanism design problem as a planning problem for link shapes, and arranging the joints along their axes of motion to be appropriately spaced and oriented such that feasible, non-intersecting paths exist linking them. Since link bending is restricted by its tubular radius, this is a Dubins planning problem, and to prove the correctness of our algorithm we also prove a theorem about Dubins paths: if two point-direction pairs are separated by a plane at least $2r$ from each, and the directions each have non-negative dot product with the plane normal, then they are connected by a radius-$r$ CSC Dubins path with turn angles $leq pi$. We implement our design algorithm in code and provide a 3D printed example of a tubular kinematic tree. The results provide an existence proof of tubular-shaped kinematic trees implementing given axes of motion, and could be used as a starting point for further optimization in an automated or algorithm-assisted robot design system.},
keywords = {},
pubstate = {published},
tppubtype = {conference}
}
Computational tools for robot design require algorithms moving between several layers of abstraction including task, morphology, kinematics, mechanism shapes, and actuation. In this paper we give a linear-time algorithm mapping from kinematics to mechanism shape for tree-structured linkages. Specifically, we take as input a tree whose nodes are axes of motion (lines which joints rotate about or translate along) along with types and sizes for joints on these axes, and a radius $r$ for a tubular bound on the link shapes. Our algorithm outputs the geometry for a kinematic tree instantiating these specifications such that the neutral configuration has no self-intersection. The algorithm approach is based on understanding the mechanism design problem as a planning problem for link shapes, and arranging the joints along their axes of motion to be appropriately spaced and oriented such that feasible, non-intersecting paths exist linking them. Since link bending is restricted by its tubular radius, this is a Dubins planning problem, and to prove the correctness of our algorithm we also prove a theorem about Dubins paths: if two point-direction pairs are separated by a plane at least $2r$ from each, and the directions each have non-negative dot product with the plane normal, then they are connected by a radius-$r$ CSC Dubins path with turn angles $leq pi$. We implement our design algorithm in code and provide a 3D printed example of a tubular kinematic tree. The results provide an existence proof of tubular-shaped kinematic trees implementing given axes of motion, and could be used as a starting point for further optimization in an automated or algorithm-assisted robot design system. |
 | Xu, Ling; Baryshnikov, Yuliy; Sung, Cynthia Reparametrization of 3D CSC Dubins' Paths Enabling 2D Search (Conference) Workshop on the Algorithmic Foundations of Robotics (WAFR), 2024. @conference{xu2024cscDubinsReparameterization,
title = {Reparametrization of 3D CSC Dubins' Paths Enabling 2D Search},
author = {Ling Xu and Yuliy Baryshnikov and Cynthia Sung},
year = {2024},
date = {2024-10-08},
urldate = {2024-10-08},
booktitle = {Workshop on the Algorithmic Foundations of Robotics (WAFR)},
abstract = {This paper addresses the Dubins path planning problem for vehicles in 3D space. In particular, we consider the problem of computing CSC paths– paths that consist of a circular arc (C) followed by a straight segment (S) followed by a circular arc (C). These paths are useful for vehicles such as fixed-wing aircraft and underwater submersibles that are subject to lower bounds on turn radius. We present a new parameterization that reduces the 3D CSC planning problem to a search over 2 variables, thus lowering search complexity, while also providing gradients that assist that search. We use these equations with a numerical solver to explore numbers and types of solutions computed for a variety of planar and 3D scenarios. Our method successfully computes CSC paths for the large majority of test cases, indicating that it could be useful for future generation of robust, efficient curvature-constrained trajectories.},
keywords = {},
pubstate = {published},
tppubtype = {conference}
}
This paper addresses the Dubins path planning problem for vehicles in 3D space. In particular, we consider the problem of computing CSC paths– paths that consist of a circular arc (C) followed by a straight segment (S) followed by a circular arc (C). These paths are useful for vehicles such as fixed-wing aircraft and underwater submersibles that are subject to lower bounds on turn radius. We present a new parameterization that reduces the 3D CSC planning problem to a search over 2 variables, thus lowering search complexity, while also providing gradients that assist that search. We use these equations with a numerical solver to explore numbers and types of solutions computed for a variety of planar and 3D scenarios. Our method successfully computes CSC paths for the large majority of test cases, indicating that it could be useful for future generation of robust, efficient curvature-constrained trajectories. |
 | Feshbach, Daniel; Chen, Wei-Hsi; Koditschek, Daniel E.; Sung, Cynthia Kinegami: Open-source Software for Creating Kinematic Chains from Tubular Origami (Conference) 8th International Meeting on Origami in Science, Mathematics, and Education (8OSME), 2024. @conference{feshbach2024kinegamiPython,
title = {Kinegami: Open-source Software for Creating Kinematic Chains from Tubular Origami},
author = {Daniel Feshbach and Wei-Hsi Chen and Daniel E. Koditschek and Cynthia Sung},
url = {https://github.com/SungRoboticsGroup/KinegamiPython
https://sung.seas.upenn.edu/research/kinegami/
https://repository.upenn.edu/handle/20.500.14332/60333},
year = {2024},
date = {2024-07-16},
urldate = {2024-07-16},
booktitle = {8th International Meeting on Origami in Science, Mathematics, and Education (8OSME)},
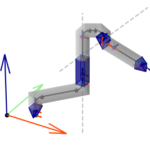
abstract = {Arms, legs, and fingers of animals and robots are all examples of “kinematic chains" - mechanisms with sequences of joints connected by effectively rigid links. Lightweight kinematic chains can be manufactured quickly and cheaply by folding tubes. In recent work [Chen et al. 2022], we demonstrated that origami patterns for kinematic chains with arbitrary numbers of degrees of freedom can be constructed algorithmically from a minimal kinematic specification (axes that joints rotate about or translate along). The work was founded on a catalog of tubular crease patterns for revolute joints (rotation about an axis), prismatic joints (translation along an axis), and links, which compose to form the specified design. With this paper, we release an open-source python implementation of these patterns and algorithms. Users can specify kinematic chains as a sequence of degrees of freedom or by specific joint locations and orientations. Our software uses this information to construct a single crease pattern for the corresponding chain. The software also includes functions to move or delete joints in an existing chain and regenerate the connecting links, and a visualization tool so users can check that the chain can achieve their desired configurations. This paper provides a detailed guide to the code and its usage, including an explanation of our proposed representation for tubular crease patterns. We include a number of examples to illustrate the software’s capabilities and its potential for robot and mechanism design.},
keywords = {},
pubstate = {published},
tppubtype = {conference}
}
Arms, legs, and fingers of animals and robots are all examples of “kinematic chains" - mechanisms with sequences of joints connected by effectively rigid links. Lightweight kinematic chains can be manufactured quickly and cheaply by folding tubes. In recent work [Chen et al. 2022], we demonstrated that origami patterns for kinematic chains with arbitrary numbers of degrees of freedom can be constructed algorithmically from a minimal kinematic specification (axes that joints rotate about or translate along). The work was founded on a catalog of tubular crease patterns for revolute joints (rotation about an axis), prismatic joints (translation along an axis), and links, which compose to form the specified design. With this paper, we release an open-source python implementation of these patterns and algorithms. Users can specify kinematic chains as a sequence of degrees of freedom or by specific joint locations and orientations. Our software uses this information to construct a single crease pattern for the corresponding chain. The software also includes functions to move or delete joints in an existing chain and regenerate the connecting links, and a visualization tool so users can check that the chain can achieve their desired configurations. This paper provides a detailed guide to the code and its usage, including an explanation of our proposed representation for tubular crease patterns. We include a number of examples to illustrate the software’s capabilities and its potential for robot and mechanism design. |
 | Chen, Wei-Hsi; Caporale, J. Diego; Koditschek, Daniel E.; Sung, Cynthia Robogami Reveals the Utility of Slot-Hopper for Co-Design of DOQ’s Body and Behavior (Workshop) ICRA 2024 Workshop on Co-design in Robotics: Theory, Practice, and Challenges, 2024. @workshop{chen2024robogami,
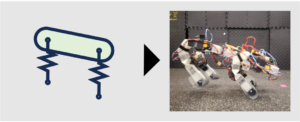
title = {Robogami Reveals the Utility of Slot-Hopper for Co-Design of DOQ’s Body and Behavior},
author = {Wei-Hsi Chen and J. Diego Caporale and Daniel E. Koditschek and Cynthia Sung},
url = {https://www.robotmechanisms.org/activities/icra-2024-codesign},
year = {2024},
date = {2024-05-13},
urldate = {2024-05-13},
booktitle = {ICRA 2024 Workshop on Co-design in Robotics: Theory, Practice, and Challenges},
keywords = {},
pubstate = {published},
tppubtype = {workshop}
}
|
 | Chen, Wei-Hsi; Qi, Xueyang; Feshbach, Daniel; Wang, Stanley J.; Kuang, Duyi; Full, Robert; Koditschek, Daniel; Sung, Cynthia Bio-inspired quadrupedal robot with passive paws through algorithmic origami design (Workshop) 7th IEEE-RAS International Conference on Soft Robotics (RoboSoft) Workshop: Soft Robotics Inspired Biology, 2024. @workshop{chen2024bio,
title = {Bio-inspired quadrupedal robot with passive paws through algorithmic origami design},
author = {Wei-Hsi Chen and Xueyang Qi and Daniel Feshbach and Stanley J. Wang and Duyi Kuang and Robert Full and Daniel Koditschek and Cynthia Sung},
url = {https://www.colorado.edu/lab/jayaram/RoboSoft2024},
year = {2024},
date = {2024-04-14},
urldate = {2024-04-14},
booktitle = {7th IEEE-RAS International Conference on Soft Robotics (RoboSoft) Workshop: Soft Robotics Inspired Biology},
howpublished = {n the workshop: Soft Robotics Inspired Biology Workshop, held in 2024 IEEE-RAS International Conference on Soft Robotics (Robosoft), San Diego, US.},
keywords = {},
pubstate = {published},
tppubtype = {workshop}
}
|
 | Chen, Wei-Hsi; Rozen-Levy, Shane; Addison, Griffin; Peach, Lucien; Koditschek, Daniel E.; Sung, Cynthia R. DOQ: A Dynamic Origami Quadrupedal Robot (Workshop) ICRA Workshop on Origami-based Structures for Designing Soft Robots with New Capabilities, 2023. @workshop{chen2023DOQ,
title = {DOQ: A Dynamic Origami Quadrupedal Robot},
author = {Wei-Hsi Chen and Shane Rozen-Levy and Griffin Addison and Lucien Peach and Daniel E. Koditschek and Cynthia R. Sung},
year = {2023},
date = {2023-05-29},
urldate = {2023-05-29},
booktitle = {ICRA Workshop on Origami-based Structures for Designing Soft Robots with New Capabilities},
keywords = {},
pubstate = {published},
tppubtype = {workshop}
}
|
 | Chen, Wei-Hsi; Yang, Woohyeok; Peach, Lucien; Koditschek, Daniel E.; Sung, Cynthia R. Kinegami: Algorithmic Design of Compliant Kinematic Chains From Tubular Origami (Journal Article) In: IEEE Transactions on Robotics, vol. 39, iss. 2, pp. 1260-1280, 2023, (Honorable mention for 2023 IEEE Transactions on Robotics King-Sun Fu Memorial Best Paper Award). @article{chen2022kinegami,
title = {Kinegami: Algorithmic Design of Compliant Kinematic Chains From Tubular Origami},
author = {Wei-Hsi Chen and Woohyeok Yang and Lucien Peach and Daniel E. Koditschek and Cynthia R. Sung},
url = {https://repository.upenn.edu/ese_papers/884/
https://www.youtube.com/watch?v=IT58JeMoAr0
https://github.com/weinitor/Kinegami},
doi = {10.1109/TRO.2022.3206711},
year = {2023},
date = {2023-04-01},
urldate = {2023-04-01},
journal = {IEEE Transactions on Robotics},
volume = {39},
issue = {2},
pages = {1260-1280},
abstract = {Origami processes can generate both rigid and compliant structures from the same homogeneous sheet material. In this article, we advance the origami robotics literature by showing that it is possible to construct an arbitrary rigid kinematic chain with prescribed joint compliance from a single tubular sheet. Our “Kinegami” algorithm converts a Denavit–Hartenberg specification into a single-sheet crease pattern for an equivalent serial robot mechanism by composing origami modules from a catalogue. The algorithm arises from the key observation that tubular origami linkage design reduces to a Dubins path planning problem. The automatically generated structural connections and movable joints that realize the specified design can also be endowed with independent user-specified compliance. We apply the Kinegami algorithm to a number of common robot mechanisms and hand-fold their algorithmically generated single-sheet crease patterns into functioning kinematic chains. We believe this is the first completely automated end-to-end system for converting an abstract manipulator specification into a physically realizable origami design that requires no additional human input.},
note = {Honorable mention for 2023 IEEE Transactions on Robotics King-Sun Fu Memorial Best Paper Award},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Origami processes can generate both rigid and compliant structures from the same homogeneous sheet material. In this article, we advance the origami robotics literature by showing that it is possible to construct an arbitrary rigid kinematic chain with prescribed joint compliance from a single tubular sheet. Our “Kinegami” algorithm converts a Denavit–Hartenberg specification into a single-sheet crease pattern for an equivalent serial robot mechanism by composing origami modules from a catalogue. The algorithm arises from the key observation that tubular origami linkage design reduces to a Dubins path planning problem. The automatically generated structural connections and movable joints that realize the specified design can also be endowed with independent user-specified compliance. We apply the Kinegami algorithm to a number of common robot mechanisms and hand-fold their algorithmically generated single-sheet crease patterns into functioning kinematic chains. We believe this is the first completely automated end-to-end system for converting an abstract manipulator specification into a physically realizable origami design that requires no additional human input. |